If you’re interested in finance, you’ve probably heard of the concepts of time value of money and valuation. But what do they mean, and why are they important?

In this blog post, I’ll explain the basics of time value of money and valuation, and how they can help you make better financial decisions. I’ll also show you some formulas and examples to illustrate how they work.

Time Value of Money

Time value of money is the idea that money today is worth more than the same amount of money in the future. This is because money today can be invested and earn interest, or be used to buy goods and services that may increase in price over time.

For example, if you have $100 today, you can invest it in a bank account that pays 5% interest per year. After one year, you’ll have $105, which is more than $100. Alternatively, you can use the $100 today to buy something that may cost more than $100 in the future, such as a movie ticket, a pizza, or a pair of shoes.

Therefore, when you compare two amounts of money that are received or paid at different times, you need to adjust them for the time value of money. This is done by using two techniques: discounting and compounding.

Discounting is the process of finding the present value of a future amount of money. Present value is the amount of money today that is equivalent to a future amount of money, given a certain interest rate. For example, if you expect to receive $100 in one year, and the interest rate is 5%, the present value of the $100 is $95.24. This means that $95.24 today is worth the same as $100 in one year, given a 5% interest rate.

Compounding is the process of finding the future value of a present amount of money. Future value is the amount of money in the future that is equivalent to a present amount of money, given a certain interest rate. For example, if you invest $100 today at a 5% interest rate, the future value of the $100 in one year is $105. This means that $100 today will grow to $105 in one year, given a 5% interest rate.

The formulas for discounting and compounding are:

For example, if you want to find the present value of $100 that you will receive in two years, and the interest rate is 5%, you can use the discounting formula:

Present value=(1+0.05)2100​

Present value=90.70

This means that $90.70 today is worth the same as $100 in two years, given a 5% interest rate.

If you want to find the future value of $100 that you invest today for two years, and the interest rate is 5%, you can use the compounding formula:

Future value=100×(1+0.05)^2

Future value=110.25

This means that $100 today will grow to $110.25 in two years, given a 5% interest rate.

Valuation

Valuation is the process of estimating the value of an asset, such as a stock, a bond, a business, or a property. Valuation is important because it helps investors, managers, and owners make informed decisions about buying, selling, or holding an asset.

There are many methods and models for valuation, but they all rely on the concept of time value of money. The basic idea is to find the present value of the future cash flows that the asset will generate, or the future cash flows that the asset will save or require.

For example, if you want to value a bond, you need to find the present value of the future interest payments and the principal repayment that the bond will provide. If you want to value a stock, you need to find the present value of the future dividends and the future stock price that the stock will offer. If you want to value a business, you need to find the present value of the future earnings and the future growth that the business will achieve.

The formulas for valuation vary depending on the type and characteristics of the asset, but they all follow the same principle: discounting the future cash flows by an appropriate interest rate, also known as the discount rate or the required rate of return.

The discount rate reflects the risk and opportunity cost of investing in the asset. The higher the risk and opportunity cost, the higher the discount rate, and the lower the present value. The lower the risk and opportunity cost, the lower the discount rate, and the higher the present value.

For example, if you want to value a bond that pays $10 in interest every year for 10 years, and then repays $100 in principal at the end of the 10th year, and the discount rate is 5%, you can use the following formula:

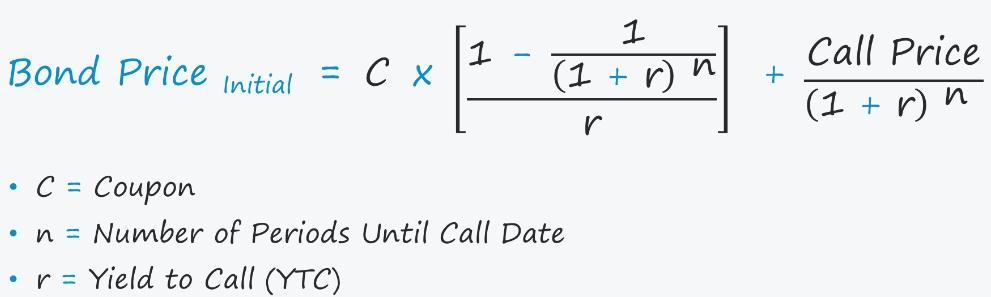
Bond value=t=1∑10​(1+0.05)t10​+(1+0.05)10100​

Bond value=77.92+61.39

Bond value=139.31

This means that the bond is worth $139.31 today, given a 5% discount rate.

If you want to value a stock that pays $2 in dividends every year, and the stock price is expected to grow by 3% every year, and the discount rate is 10%, you can use the following formula:

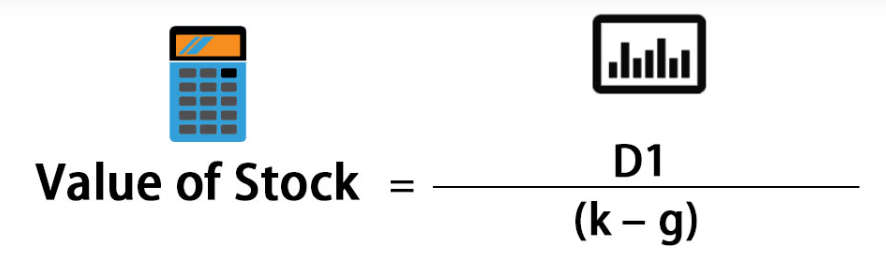
Stock value=0.10−0.032​

Stock value=28.57

This means that the stock is worth $28.57 today, given a 10% discount rate and a 3% growth rate.

Conclusion

Time value of money and valuation are two fundamental concepts in finance that can help you understand and compare the value of different assets and investments. By using the techniques of discounting and compounding, and the formulas of valuation, you can make better financial decisions and achieve your financial goals.